隣接行列，接続行列，ラプラシアン行列

グラフについてはグラフ理論の基礎をどうぞ。

以下では単純無向グラフ $G=(V,E)$ について考えます。ただし，$V$ は $G$ の頂点集合，$E$ は枝集合を表します。

各行，列がそれぞれ頂点に対応しており，枝がある部分に $1$ ，ない部分に $0$ を格納した $|V|\times |V|$ の正方行列を隣接行列と言います。

例

図のグラフ $G$ に対応する隣接行列は，$A=\begin{pmatrix}0&0&0&0\\0&0&1&1\\0&1&0&1\\0&1&1&0\end{pmatrix}$

隣接行列 $A$ の性質

• $A$ は対称行列
• $A^n$ の $ij$ 成分は，$G$ における $i$ から $j$ への長さ $n$ の道（同じところを複数回通ってもよい）の本数

各行が頂点，各列が枝（辺）に対応しており，頂点が枝に接続しているときは $1$ ，そうでない部分に $0$ を格納した $|V|\times |E|$ の行列を（点枝）接続行列と言います。

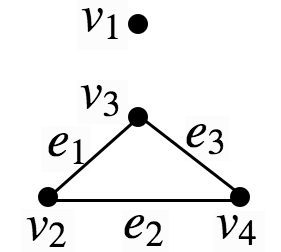
例

図のグラフに対応する接続行列は，$Q=\begin{pmatrix}0&0&0\\1&1&0\\1&0&1\\0&1&1\end{pmatrix}$

なお，有向グラフの場合，枝が頂点から出て行く部分は $1$ ，入ってくる部分は $-1$ とする場合が多いです(※)。

接続行列 $Q$ の性質

• （無向グラフにおいて）二部グラフの接続行列は完全単模（任意の正方部分行列の行列式が $0$ または $\pm 1$）

• （有向グラフにおいて※のように接続行列を定めた場合）任意のグラフの接続行列は完全単模

各行，列がそれぞれ頂点に対応しており，対角成分にはその頂点の次数，非対角成分については枝がある部分に $-1$ ，ない部分に $0$ を格納した $|V|\times |V|$ の正方行列をラプラシアン行列（グラフラプラシアン）と言います。

例

さきほどの図のグラフに対応するラプラシアン行列は，

$L=\begin{pmatrix}0&0&0&0\\0&2&-1&-1\\0&-1&2&-1\\0&-1&-1&2\end{pmatrix}$

ラプラシアン行列 $L$ の性質

• $L$ は対称行列
• $L$ の各行，各列の和は $0$
• $\mathrm{rank}\:L=|V|-1$ $\iff G$ が連結
• $L$ の任意の余因子は $G$ の全域木の個数と等しい（行列木定理）

各行，列がそれぞれ頂点に対応しており，頂点 $i$ と $j$ を結ぶ枝があるとき，$ij$ 成分に変数 $x_{ij}$ を，$ji$ 成分に $-x_{ij}$ を格納した行列（他の成分は $0$ ）をTutte行列と言います。

例

さきほどの図のグラフに対応するTutte行列は，

$T=\begin{pmatrix}0&0&0&0\\0&0&x_{23}&x_{24}\\0&-x_{23}&0&x_{34}\\0&-x_{24}&-x_{34}&0\end{pmatrix}$

Tutte行列 $T$ の性質

• $T$ は歪対称行列
• $T$ が正則 $\iff$ $G$ に完全マッチングが存在
• $\dfrac{1}{2}\mathrm{rank}\:T=G$ の最大マッチングのサイズ