法線ベクトルの3通りの求め方と応用
点 における法線とは, を通り接線に垂直な直線のことです。
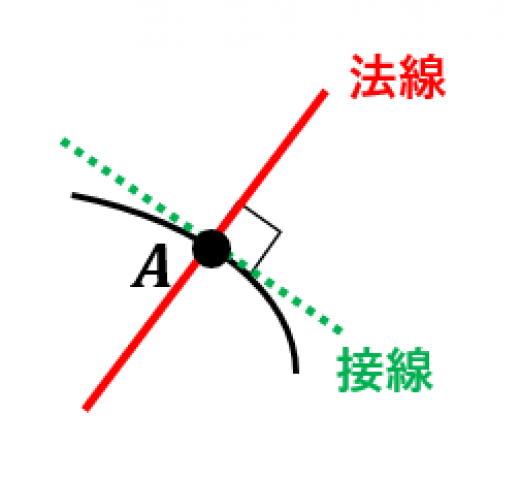
この記事では法線に関するいろいろな公式を紹介します。
- 直線の方程式と法線ベクトル
- 法線の方程式を計算する公式
- 法線方向のベクトル(法線ベクトル)を偏微分で計算する公式
- 媒介変数表示された曲線の法線ベクトルを計算する公式
復習:直交する2直線の関係
復習:直交する2直線の関係
2直線 , が直交するのは となるときである。
直線とその法線ベクトル
直線とその法線ベクトル
直線から法線ベクトル
直線 の法線ベクトルは (の定数倍)である。
直線の式を変形すると です。「垂直な2直線の傾きの積は 」であるため,直交する直線の傾きは です。
よって法線ベクトルは です。
法線ベクトルから直線
法線ベクトルが で を通る直線は である。
ベクトル は直線の傾きと平行なベクトルです。
このベクトルと法線ベクトルが直交することから,これらの内積は です。よって 整理すると となります。
法線の方程式の求め方
法線の方程式の求め方
まずは,座標平面における法線の方程式を求める方法を紹介します。
の における接線の傾きは です。そして「垂直な2直線の傾きの積は 」なので法線の傾きは となります。よって,以下が成立します。
の における法線の方程式は なら
の における法線の方程式を求めよ。
より, です。
よって法線の方程式は,上の公式より , つまり となります。
法線ベクトルの求め方
法線ベクトルの求め方
次は,法線ベクトルを求める一般的な公式を紹介します。法線ベクトルとは,法線方向(接線に垂直な方向)のベクトルです。
「偏微分」という名前と記号を見て一瞬ひるんでしまいがちですが,意味は単純です。多変数関数を特定の変数に関して微分したものを偏微分と呼ぶだけです。 と書いたり と書いたりします。公式の証明は後ほどします。
の における法線ベクトルを計算せよ。
は と変形できます。そこで として公式を使います。
- で偏微分すると となる。 のとき
- で偏微分すると となる。
よって,法線ベクトルの1つは
の における法線ベクトルを求めよ。
より における偏微分の値は となる。よって が法線ベクトルの つ。
このように,どんな関数でも, の形に直して各変数で微分してその点の座標を代入することで法線ベクトルが簡単に求まります!
法線ベクトルの公式の応用
法線ベクトルの公式の応用
法線ベクトルの知識は大学入試でも役立ちます。例えば,法線ベクトルが分かれば接線の方程式が分かります。
ここでは応用例として, 円 : 上の点 における接線の方程式を導出します。
の における法線ベクトルは上記の公式を用いて と分かる。
よって,
が接線上にある
と法線ベクトルが垂直
となり円の接線の方程式を得る。
これでも十分ですが,見慣れた形に変形してみます:
→
(ここで
であることを用いた)
同様に楕円,双曲線などの接線の方程式も簡単に求めることができます。
また,法線ベクトルの他の応用としては平面の方程式が挙げられます。 →平面の方程式とその3通りの求め方
法線ベクトルの公式の導出
法線ベクトルの公式の導出
法線ベクトルの公式を導出します。つまり「各成分の偏微分を並べたベクトル」が法線ベクトルになっているという主張を示します。この「各成分の偏微分を並べたベクトル」は 勾配ベクトルと呼ばれ,大学数学や物理で大活躍します。→勾配ベクトルの意味と例題
大雑把な説明をします( 論法を用いた厳密な証明は大学範囲です)。
曲線 上の点 からほんの少し動いた点 も同じ曲線上にあるとする。 が十分小さいとき における接線の方向ベクトルは とみなせる。
これと直交するベクトルを求めるのが目標。
ここで, の近くで 方向に だけ進むと関数値は 増える(一次近似)。
同様に の近くで 方向に だけ進むと関数値は 増える
ところが における関数値はともに で等しいので
これは勾配ベクトル と接線ベクトルの内積が であることを示しており,勾配ベクトルと接線ベクトルは直交することが分かる。
曲線の法線ベクトル
曲線の法線ベクトル
曲線 における法線ベクトルは,
もう少し丁寧に言うと,媒介変数 を用いて と表される曲線の における法線ベクトルは, になります。
で表される曲線の での法線ベクトルを求めよ。
において なので,法線ベクトルの1つは
を だけ変化させたときに曲線上の点は から に変化する。 が小さいとき,変化後の点の座標は
と近似できる。よって,接線方向のベクトルの1つとして が取れる。
法線ベクトルはこれを90°回転させればよいので,回転行列 をかけると となる。
勾配ベクトルは大学数学のベクトル解析でより深く学びます。
Tag:偏微分の高校数学への応用











