四色定理の紹介と五色定理の証明
任意の地図は四色で塗り分けることができる。
四色定理について
四色定理について
-
地図の各領域に色を塗りたい,そのとき隣り合う領域は同じ色にはしたくないという状況を考えます。アメリカの本土とアラスカのような飛び地は考えません,一つの面を一つの色で塗ります。

-
図は非常に単純な例ですが,地図がどんなに複雑でも四色で塗れる! というのが四色定理です。主張が非常にシンプルで美しいため有名な定理です。
-
証明は非常に複雑(コンピュータを使った力技が必要)です。一方,五色定理(四色定理の主張の「四色」を「五色」に変えた弱い定理)は証明が一気に簡単になり,高校生でも理解できます。というわけで,この記事では五色定理の証明を解説します。
準備:平面グラフの頂点彩色に帰着
準備:平面グラフの頂点彩色に帰着
与えられた地図に対して,以下のようなグラフ を構成します(→グラフ理論の基礎)。
- の頂点は地図の面に対応。
- 地図で隣接している面同士に枝を引く。

そして「隣接する領域が異なる色になるように,五色で地図の面を塗る」という当初の目標を「どの枝の両端点も異なる色になるように,五色で の頂点を塗る」と言い換えます。
が平面的グラフ(平面に交差なしで書けるグラフ,→平面グラフ・平面的グラフの意味とオイラーの定理の応用)になることに注意すると,以下の定理を証明すればよいことが分かります。
平面的グラフは五彩色可能(五色あればどの枝の両端点も異なる色になるように頂点を塗れる)。
準備2:次数5以下の頂点の存在
準備2:次数5以下の頂点の存在
五色定理の証明の準備その2です。
平面的グラフには次数(隣接する頂点数)が 以下の点が必ず存在する。
平面的グラフ の全ての頂点の次数が 以上と仮定する。 の頂点数,枝数,面の数をそれぞれ とする。
各頂点に 本以上枝が集まるので,
各面の境界に含まれる枝数は 以上なので
これらの不等式とオイラーの多面体定理より,
となり矛盾。背理法により補題が示された。
五色定理の証明
五色定理の証明
以上の準備をふまえ,平面的グラフ が五彩色可能であることを に関する帰納法で証明します。
のときは自明。以下, のときを仮定して のときを証明する。
には補題より次数 以下の頂点が存在する,そのうちの一つを とする。 から (および に接続する枝)を除いたグラフを とする。帰納法の仮定により は五彩色可能である。この彩色で の 以外の頂点を塗る。
(i) の次数が であり,その つの頂点が全て異なる色で塗られている場合:
つの頂点を とし,各頂点の色を とする。
から色 と で塗られた頂点のみをつたって行ける頂点の集合を と書く。
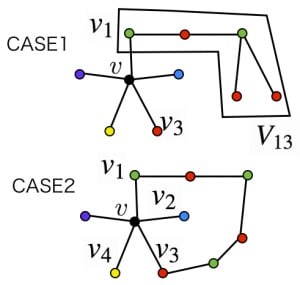
CASE1: のとき,
の色 と をひっくり返せば彩色の条件を保ったまま の周りを四色にできる。 を で塗ればよい。
CASE2: のとき,
から に と で塗られた頂点のみからなる道が存在する。
これと の平面性から, から に と で塗られた頂点のみからなる道は存在しない。
つまり, から色 と で塗られた頂点のみをつたって行ける頂点の集合 の色 と をひっくり返せば の周りが四色になる。 を で塗ればよい。
(ii) そうでない場合:
余った色で を塗ればよい。
四色と言えば迷わず赤黄青緑ですが,五色目を何色にするか迷いました。











