三角形のフェルマー点の3通りの証明
-
三角形 の各頂点からの距離の和 を最小にする点 をフェルマー点と言う。
-
最大角が 未満の三角形 において,フェルマー点は三角形の内部に存在して
フェルマー点とは
フェルマー点とは
三角形 において,三頂点からの距離の和 を最小にする点をフェルマー点といいます。距離の和を最小にするというのは工学的にも重要です。例えば「三軒の家に電線を使って電気を配給するときに,どこに電柱を立てれば電線の長さを短くできるか?」といった問題です。
このページではフェルマー点が を満たす点であることを3通りの方法で証明します。
- 初等幾何を用いた有名な方法
- 楕円の性質を用いた方法
- トレミーの定理を用いた方法
2では楕円の反射定理を,3ではトレミーの不等式を前提知識として用います。3つとも面白いですが,個人的には2番目の方法がおすすめです。
- 初等幾何によるフェルマー点の証明
- 初等幾何によるフェルマー点の証明
線分の和を最小化する問題は多くの場合 線分和を同じ長さの折れ線に移して,「折れ線は直線のときに最小になる」という性質を用いることで解決します。
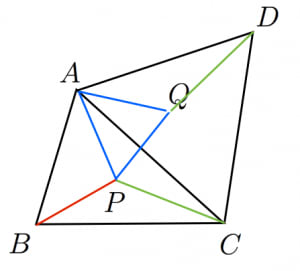
三角形の内部の点を とする。 と頂点 を 「 を中心として反時計回りに 回転させた点」を とおく。三角形 は正三角形となる。
三角形 と は2辺とその間の角がそれぞれ等しいので合同となり,
よって,
この不等式は任意の内部の点 に対して成立する。
三角形 の最大角が 未満のとき,内部の点 をうまく選ぶと がこの順で一直線上に並び,上記不等式で等号が成立する。このとき,
ちなみに,三角形の最大角が 以上のとき
- がこの順で一直線上になるような内部の点 をとることはできません。例えば, のとき 線分 は三角形の内部を通りません。
- フェルマー点は最大角の頂点と一致することが知られています。
- 楕円の性質を用いたフェルマー点の証明
- 楕円の性質を用いたフェルマー点の証明
線分の和が一定となる軌跡は楕円です。楕円の性質をうまく用いるとフェルマー点が簡単に導けます。前提知識として楕円の反射定理(→楕円の反射定理とその証明)が必要になります。

が一定となる軌跡は を焦点とする楕円 。
よって, が一定のもとで が最小になるのは, における の接線と が直交するとき。
このとき,楕円の反射定理より, となる。同様にして, がフェルマー点となるとき が分かる。
狐につままれたような証明ですが,楕円の性質をきちんと理解していればこの証明が一番簡潔でわかりやすいと思います。「焦点から光線を打つと壁に反射して反対側の焦点に到達する」という楕円の性質を利用しています。
- トレミーの不等式を用いたフェルマー点の証明
- トレミーの不等式を用いたフェルマー点の証明
以下のトレミーの不等式を用います。
平面上の任意の4点 に対して,
等号成立条件は, がこの順番に円周上にあるとき。

直線 に関して と反対側に,三角形 が正三角形となるように点 を取る。
トレミーの不等式より, となり,
等号が成立するのは, が同一円周上にあり, が一直線上にあるとき。
このとき,
同様にして も示せる。
トレミーの不等式の証明は長くなるので,気になる人は以下を参照してください。 →トレミーの不等式の証明と例題
トレミーの定理を正三角形に適用するのは,トレミーの定理とその3通りの証明,応用例の応用例3の構図で頻出なのでなんとなく覚えておくとよいでしょう。
ちなみに……解析幾何(座標計算,ベクトル計算をゴリゴリする)でも頑張って証明しようとしたのですが,挫折しました。やはり角度が絡む問題は座標で扱うのは厳しいようです。
2013年の東大の入試問題でもフェルマー点に関する問題が出題されています。
Tag:三角形の五心に関する定理まとめ
Tag:有名な定理を複数の方法で証明











