指数分布の意味と具体例
指数分布とは,ランダムなイベントの発生間隔を表す分布です。指数分布は「地震が起きる間隔」や「電球の寿命」などを表す分布として使われます。
この記事では,指数分布の意味や指数分布とポアソン分布との関係などについて解説します。
指数分布の例と重要性
指数分布の例と重要性
指数分布とは,ランダムなイベントの発生間隔を表す分布です。「ランダムなイベント」とは大雑把に言うと「起こる確率が常に一定である」ようなイベントのことです。例えば,
- 地震が起きる間隔
- 電球の寿命
- 人とすれ違うタイミングの間隔
などは(おおよそ)指数分布に従うと言えます。
指数分布の確率密度関数
指数分布の確率密度関数
(平均が である)指数分布の確率密度関数は
となります。
例えば,寿命が「平均 時間の指数分布」に従う電球について,寿命が 時間以下となってしまう確率は,
のように計算できます(つまり,約 %であることが分かります)。
指数分布のグラフ
指数分布のグラフ
指数分布の確率密度関数 のグラフは以下のようになります。
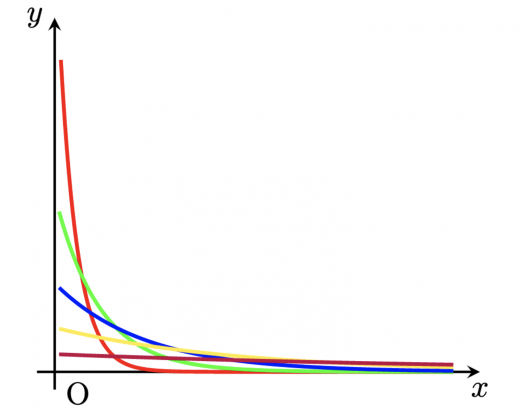 の場合を描いています。色は順番に,赤,緑,青,黄,紫です。グラフから,
の場合を描いています。色は順番に,赤,緑,青,黄,紫です。グラフから,
- がどの値でも単調減少
- が大きいほど右に寄る(つまり平均が大きくなる)
ことがわかります。
ポアソン分布との関係
ポアソン分布との関係
ランダムな(いつ起こるか分からない,不定期な)イベントは世の中にたくさんあります。指数分布・ポアソン分布はともに,そのようなイベントに関連した分布です。
(長い時間平均すると)時間 あたり1回起こるような「ランダムなイベント」について,
1. イベントの発生間隔は平均 の指数分布に従う
2. 単位時間にイベントが起きる回数は平均 のポアソン分布に従う
発生間隔が長いほど,発生回数は小さくなることに注意してください。
ランダムな現象を「発生間隔で捉えると指数分布,発生回数で捉えるとポアソン分布」と覚えておきましょう。
2についてはポアソン分布の意味と平均・分散で詳しく解説しています。1については以下で証明します。
指数分布の式の導出
指数分布の式の導出
では,なぜ「ランダムなイベントの発生間隔」を表す分布が,確率密度関数が
である指数分布になるのでしょうか?
少し難しいですが,これを証明してみます。
が十分小さいとき,時刻 から の間にイベントが発生する確率を二通りの方法で求める。
・確率密度関数の定義により
・(時刻 までイベントが起こらない確率)×(それから の間に起こる確率)
=
ただし「発生間隔の平均が であるランダムなイベント」が「時間 の間に起こる確率」は であることを用いた。
よって,
両辺を で微分すると,
この微分方程式を解くと,
確率密度関数であるので となるように定数 を定めると, を得る。
つまり,
※求める確率密度関数が滑らか(微分可能)であることは仮定しました。
幾何分布との関係
幾何分布との関係
指数分布は連続型確率分布です。指数分布の離散バージョンが幾何分布です。
指数分布も幾何分布も「無記憶性」を持ちます。 →幾何分布の具体例と期待値,無記憶性について
確率密度関数であることの確認
確率密度関数であることの確認
指数分布は確率密度関数が比較的単純なので,分布のいろいろな量を求めるよい計算練習になります。そのため,各種試験(アクチュアリー,大学院入試など)に頻出,という意味でも重要です。
例えば,指数分布の確率密度関数:
が確かに確率密度であることを確認します。
よりOK。
指数分布の期待値
指数分布の期待値
指数分布の平均(期待値)が であることを確認します。
証明には部分積分,および を用います。
指数分布の分散
指数分布の分散
指数分布の分散が であることを確認します。
よって,
3日間誰からもメールが来ない寂しい時期もあれば,1日に大量にメールが来る日もあるのが納得できます。










