エルデス・モーデルの定理の証明

任意の三角形 において,その内部の任意の点 から各辺に下ろした垂線の足を とおくとき,以下の不等式が成立する。
エルデスモーデルの定理(エルデシュモーデルの定理)は美しい幾何不等式です。点 を動かすと6本の線分の長さが同時に全て変化してしまうので,証明するのは意外と難しいです,数学オリンピック対策にどうぞ。
証明の準備
証明の準備
実は,エルデスモーデルの定理よりも強い幾何不等式が成り立ちます。
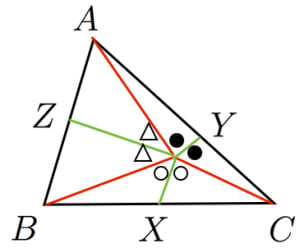
の二等分線と辺 の交点を とおきます。 も同様に定義します。
すると, が成立するので,
が示せればエルデスモーデルの不等式が証明されます。
すなわち,赤 2青 の代わりに赤 2緑を示せば良いわけです。
表記簡略化のために ,,,,,,,, とおきます。
エルデスモーデルの定理の証明
エルデスモーデルの定理の証明
角の二等分線があるので,角の二等分線に関する重要な3つの公式の2番を用いて必要な関係式を導出します。次に, を上から抑えたいので相加相乗平均の不等式を用います。あとは機械的な計算です。
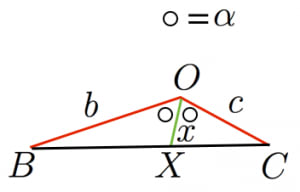
三角形 に注目して,角の二等分線を含む三角形の公式から
である。よって,相加相乗平均の不等式より,
同様に,
よって,以下の不等式を示せば良い:
(注:これは の場合のKlamkinの不等式である。)
これを に関する二次不等式とみると,判別式が0以下であることが必要十分である。
整理すると以下と同値である。
ここで, より, であり,加法定理を用いて上の不等式をさらに同値変形する。
これは成立する。
(1) は, に関する2次不等式なので簡単に証明できます。平方完成や判別式による方法,二次形式を知っている人は行列式を調べることでも証明できます。上記の証明では判別式による方法を用いています。
コメント
コメント
-
エルデスモーデルよりも強い幾何不等式に帰着させるのが一番の難所です。
慣れている人なら,角の二等分線定理による式変形,相加相乗平均の不等式,二次不等式の話などを思いつくのは難しくないと思います。 -
エルデスモーデルの不等式は,オイラーの不等式: となんとなく似ています。
一つ一つの道具が簡単でも最後まで証明をやり抜くのはむずかしい。
Tag:幾何不等式の解法パターンまとめ











