イプシロンデルタ論法とイプシロンエヌ論法
更新
イプシロンデルタ論法,イプシロンエヌ論法について解説します。関数や数列の極限を厳密に扱うために必要な道具です。大学数学最初の難関の1つです。
関数の極限の厳密な定義
関数の極限の厳密な定義
まずは,イプシロンデルタ論法による関数の極限 の定義です。
任意の正の実数 に対して,ある正の実数 が存在して, なら
が成立するとき, とする。
赤字の主張は意味がわかりにくいですね。これを理解するために,高校数学における極限の大雑把な意味を思い出してみます。
が限りなく に近づくとき, は限りなく に近づくとき, とする。
紫字の主張はわかりやすいです。これを1→2→3の順で徐々に言い換えてみましょう。
-
が限りなく に近づくとき, が限りなく に近づく
-
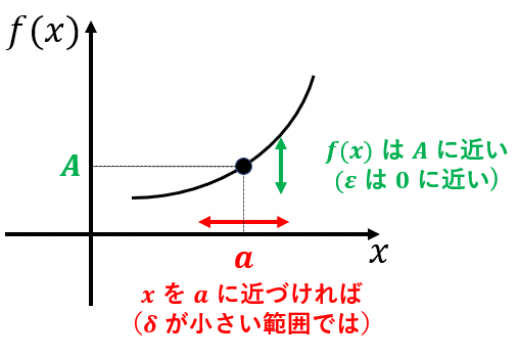
どんなに小さな正の に対しても を十分 に近づければ となる
-
任意の正の実数 に対して,ある正の実数 が存在して, なら
イプシロンデルタ論法の使用例
イプシロンデルタ論法の使用例
を確認せよ。
が限りなく に近づくとき, も限りなく に近づくことは明らかですが,イプシロンデルタ論法による極限の定義をきちんと確認してみましょう。
任意の正の実数
に対して,ある正の実数
が存在して,
なら
(*)
を確認するのが目標。
- もし と言われたら, とすれば(*)を満たす。
- もし と言われたら, とすれば(*)を満たす。
- より一般に,与えられた に対して とすれば(*)を満たすのでOK。
他のいろいろな極限の定義
他のいろいろな極限の定義
の定義さえきちんと理解できれば,他の定義もすんなり受け入れられる(自分で構成できる)と思います。
関数の極限
(正の無限大に発散)の意味は,
任意の実数 に対して,ある が存在して, なら
(負の無限大に発散)の意味は,
任意の実数 に対して,ある が存在して, なら
(無限大に行くときの極限)の意味は,
任意の に対して,ある が存在して, なら
数列の極限
の意味は,
任意の に対して,ある が存在して, なら
※ 任意の に対して を取ってくるのがイプシロンデルタ論法でした。数列の極限では,任意の に対して を取ってくるのでイプシロンエヌ論法ということが多いです。
, , などについても考えてみてください。
使用例
使用例
イプシロンデルタ論法に慣れるためにはいろいろな証明を読んだり,自分で問題を解くのが一番です。ここでは3つ例を紹介します。
-
関数の連続性と一様連続性
イプシロンデルタ論法を用いて,関数の連続性について議論します。 -
はさみうちの原理の証明
イプシロンエヌ論法を用いて(直感的にも当たり前と思える)事実をきちんと証明します。 -
チェザロ平均の性質と関連する東大の問題
イプシロンエヌ論法を用いて(直感的にはすぐには分からないかもしれない)事実をきちんと証明します。
また,いくつか例題を載せた記事もあります。是非チェックしてみてください。
展望
展望
イプシロンデルタ論法は「近傍」によって連続性を理解するものと言えます。これは距離空間というアイデアに拡張されていきます。
詳しくは 距離空間~位相空間論に向けた開集合・閉集合の一般化 を読んでみてください。
イプシロンアール論法とはあまり言わないです。











