二次曲線の分類(四通りの方法)
二次曲線(または円錐曲線)と呼ばれる,楕円・放物線・双曲線について統一的に解説します。母線・離心率・行列式・エネルギーといういろいろな観点で分類することで,二次曲線の理解を深めます。
円錐を切る角度による分類
円錐を切る角度による分類
- 円錐を平面で切った切り口は,二次曲線(楕円・放物線・双曲線)になります。そのため,二次曲線は円錐曲線とも呼ばれます。

- 図の青い曲線が楕円の場合を示しています。
- 無限に大きな同じ二つの円錐を持ってきて,そのうち一つをひっくり返した図形(図では灰色の領域を点線を中心に回転させたもの)を考えます。
- この図形を平面で切るとき「母線の傾き」と「切る平面の傾き」の大小関係で円錐曲線が分類できます。
- 平面が母線より緩いとき楕円
- 平面が母線より急なとき双曲線
- 平面が母線と平行なとき放物線
円錐を切る様子を3通りイメージしてみてください。
式による分類
式による分類
-
平面上で という式が表す曲線は一般に楕円,放物線,双曲線のいずれかです(直線,二直線,解なしなどつまらない例もある)。二次曲線と呼ばれる理由です。
-
高校数学では, の場合以外はほとんど登場しません。
楕円:
双曲線:
放物線: -
(上記のつまらない例でないもとで) の符号を見ることで二次曲線を分類できます:
- のとき楕円
- のとき双曲線
- のとき放物線
-
分類の証明は,「回転と平行移動を適切に行うことで曲線を という形に変換する」ことでできます。高校数学でできないこともないですが,大学の線形代数で固有値,直交変換あたりの概念を習うとスッキリと理解できます。→斜めの楕円の方程式(特に45度回転)
-
変数の数がもっと増えた場合は行列のシルベスター標準形というものを考えることになります。
離心率(軌跡)による分類
離心率(軌跡)による分類
- 直線 と点 からの距離の比が で一定であるような点の軌跡は二次曲線となります。簡単な計算で証明できます。
- の場合が特に有名です。→放物線の準線・焦点と一般化
- を離心率と言います。離心率を用いて二次曲線を分類できます。
- のとき楕円
- のとき双曲線
- のとき放物線
詳しくは,以下の記事で解説しています。
エネルギーによる分類
エネルギーによる分類
離心率とほぼ同じことですが,物理的な見方もできます。地球が太陽を焦点の一つとする楕円軌道を描いていることは有名ですね。→地球の公転軌道が楕円であることの導出
力学において,二体問題の解軌道は二次曲線になります。例えば,宇宙空間に地球と太陽しかないと仮定すると地球の軌道は二次曲線になります。厳密には他の星とかも影響するので微妙にずれます。
このとき描く軌道は両者が持つエネルギーで分類できます。簡単のため片方の星が静止している場合を考えます。もう片方の星のエネルギーを とおくと以下が成立します。
- のとき楕円
- のとき双曲線
- のとき放物線
のとき,万有引力による束縛が強いためぐるぐる回ります。 のとき,星のスピードが速すぎて二度と戻ってきません。
まとめ
まとめ
二次曲線(円錐曲線)の4つの観点での分類を紹介しました。
- 切る平面の傾き
- 離心率
- エネルギー
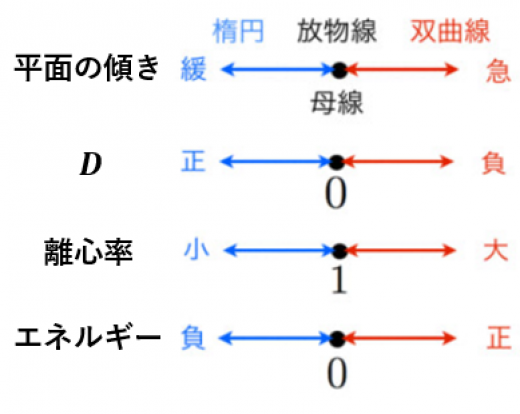
放物線はいろいろな意味で,楕円と双曲線の境界にいることがわかります。











