道順の場合の数を求めるテクニック

まずは最短経路問題の最も基本的なタイプです。

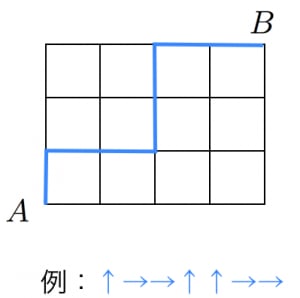
まずは教科書的に解きます。→と↑の列を考えます。

道順の場合の数を求める別解を解説します。「書き込み方式」などと呼ばれるものです。

点 $A$ から頂点 $P$ にたどりつくための最短の道順の数を $N(P)$ と書きます。目標は $N(B)$ を求めることです。

書き込み方式では $A$ の近くの頂点から順々に，各頂点 $P$ に $N(P)$ を書いていきます。

具体的には $N(P)$ は，$P$ の左の頂点を通る最短経路の数と，$P$ の下の頂点を通る最短経路の数の和です。 よって，左の頂点の数字と下の頂点の数字を足したものを $P$ に書いていきます。例えば青い点に行くには赤い点か緑の点のどちらか一方のみを通るので $4+6=10$ を青い点に書きます。

ただし，一番下の行と左の列の頂点に関しては最短経路は一通りです。

与えられた問題設定が複雑になればなるほど書き込み方式は威力を発揮します！

例えば以下のような場合，矢印の列との対応を考えるのはかなり大変になりますが，書き込み方式は使えます。

• 全体が長方形でない
• 通ってはいけない点が指定されている（穴がある，池がある，工事中など）

書き込み方式は簡単な漸化式を使って場合の数の問題を解いた，とみなせます。

このように「漸化式を利用して次々に途中までの解を記録していき最終的に解を求める方法」を計算機科学の専門用語で 動的計画法と言います。

動的計画法の（大学入試に出そうな）他の応用としては「階段を上る場合の数」があります。

ちなみに各 $a_n$ はフィボナッチ数になります。→フィボナッチ数列の7つの性質（一般項・黄金比・互いに素）

→高校数学の問題集　～最短で得点力を上げるために～のT59では，この例題の3通りの解法を紹介しています。