深さ優先探索と幅優先探索
更新
深さ優先探索とは「とにかく行けるとこまで行ってそれ以上進めなくなったら一歩戻ってそこから探索する」という探索方法。
幅優先探索とは「出発点に近い点から順に探索する」という探索方法。
この記事では「深さ優先探索」「幅優先探索」について解説します。非常に基本的なグラフ探索のアルゴリズムです。
深さ優先探索,幅優先探索でやりたいこと
深さ優先探索,幅優先探索でやりたいこと
深さ優先探索や,幅優先探索は,グラフ探索に使えるアルゴリズムです。
グラフ探索とは,グラフ(ネットワーク)の頂点を全て探索したい,という問題です。
ただし,グラフは連結(どの頂点からどの頂点までもたどりつける)とします。
深さ優先探索
深さ優先探索
深さ優先探索(depth-first search, DFS)は大雑把に言うと,とにかく行けるとこまで行ってそれ以上進めなくなったら一歩戻ってまた探索するという方法です。
頂点 から出発してアルファベット順に探索する。
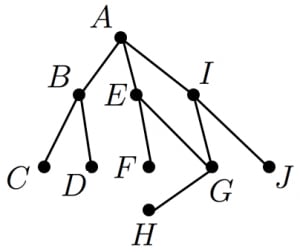
具体的な手順は,
- ぶつかるまで未訪問の頂点を適当に進む
- 必要なだけ戻る
- ぶつかるまで未訪問の頂点を適当に進む
- 必要なだけ戻る
- ぶつかるまで未訪問の頂点を適当に進む
- 以下同様
「一番最近(最後に)見たものの周りを最初に探索する」という方針です。last in, first outと言うこともあります。実装にはスタックというデータ構造を使います。カップスタックというカップを積み重ねる競技を知っているとイメージしやすいでしょう。
なお,深さ優先探索は迷路の解法にも使えます(壁に沿って進む感じ)。
幅優先探索
幅優先探索
幅優先探索(breath-first search, BFS)は大雑把に言うと,出発点に近い点から順に探索するという方法です。
頂点 から出発してアルファベット順に探索する。

具体的な手順は,
- に隣接しているものを探索する()
- に隣接しており未訪問のものを探索する()
- に隣接しており未訪問のものを探索する()
- 以下同様
「一番最初に見たものの周りを最初に探索する」という方針です。first in, first outと言うこともあります。実装にはキューというデータ構造を使います。
計算時間
計算時間
深さ優先探索または幅優先探索を使うことで,頂点数 ,辺の数 のグラフの頂点は線形時間(高々 に比例する時間)で探索できます。
辺の数が一億本などの巨大なグラフでも,コンピューターを使えば探索することができます!
「Facebookの友達グラフ」などのもっと巨大なグラフになると線形時間でも遅いようです。











