平均値，中央値，最頻値の求め方といくつかの例

• 平均値，中央値，最頻値は，いずれもたくさんの数を1つの数で「代表する」ための値です。「代表値」と呼ばれます。

• どの代表値を使うべきかは状況によります。以下のメリット・デメリットを理解しておきましょう（それぞれの後で詳しく説明します）。

データの値の算術平均（全部足してデータ数で割ったもの）を平均値と言います。最も有名な代表値です。

ほとんどの人が $10$ 点以下なのに一人の天才によって平均点が $10$ 点以上も上がってしまいました。

度数分布表と平均値

データが度数分布表にまとめられている場合は，「度数」と「階級値」を用いて平均値を近似的に求めることができます。具体的には，階級が $n$ 行あり，$i$ 行目の階級値を $x_i$，度数を $c_i$ とすると，平均値は以下の値に近くなります。

$$\dfrac{x_1c_1 + x_2c_2 + \cdots + x_nc_n}{c_1 + c_2 + \cdots + c_n}$$

データを大きい順（または小さい順）に並べたとき，真ん中の値を中央値（メディアン）と言います。データの数が偶数のときは「真ん中の値」が二つ登場するのでそれらを足して2で割ったものを中央値とします。

データの中で最も頻度が高い値を最頻値（モード）と言います。

この例で $52$ 点の人が $53$ 点になると最頻値による分析はできなくなります。また，$52$ 点の人が $70$ 点になると最頻値は $70$ 点になってしまいます。

この例のようにサンプルサイズが少ないとき，データがぴったり一致することは珍しいので変なところ（感覚とズレるところ）に最頻値が来ることがあります。そのためそのまま最頻値を使うのは得策ではありません。

そこで，データを度数分布表・ヒストグラムにした上で度数が最も大きい階級の階級値を最頻値とすることもあります。

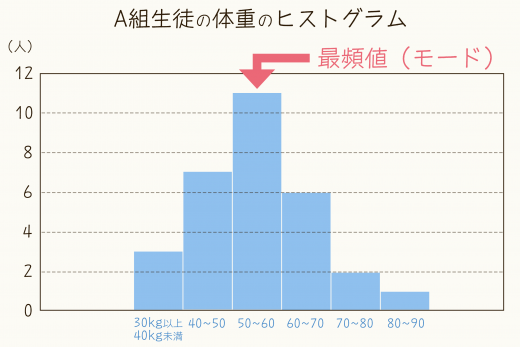
ヒストグラムと最頻値

ヒストグラムから最頻値を求める場合，「最も度数の多い階級の階級値」を最頻値とみなすことがあります。最も山が高くなっている部分が最頻値です。

対称で山が一つ（単峰性）の分布では平均値，中央値，最頻値はほとんど同じ値なのでどれを使っても問題ないことが多いです（上側の図，横軸はデータの値，縦軸はデータの頻度を表す）。

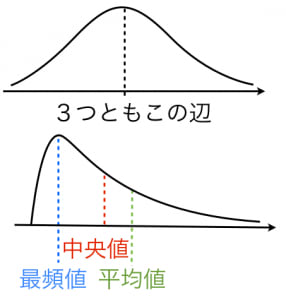
山が一つでも対称でない（偏っている）分布のときは 平均値が外れ値に引っ張られ「平均値，中央値，最頻値」の順に並ぶことが多いです（ピアソンの経験則）。例えば所得の分布もこのような構造をしていると考えられます（年収1億とかの人が平均年収をつりあげている，下側の図）。

以上のように，代表値は分布の特徴を表す重要な指標ですが， 一つの代表値だけで判断するのは危険です。背後にある分布がどのような形なのか意識するべきです。

Tag:数学1の教科書に載っている公式の解説一覧