楕円の接線を求める公式とその証明
更新
楕円 上の点 における接線の方程式は,
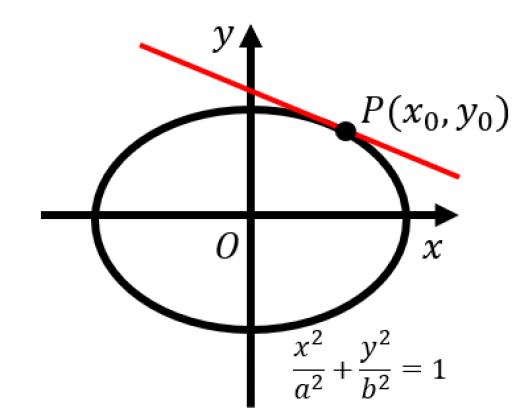
楕円の接線を求める公式について
楕円の接線を求める公式について
-
楕円の方程式 において , とすれば楕円の接線の方程式になります。覚えやすいです。
-
の場合は円の接線の方程式を求める公式になります。→円の接線の方程式を求める公式の3通りの証明
以下では,楕円の接線の方程式を求める方法(冒頭の公式の証明)を2通り解説します。
傾きと通る1点から求める方法
傾きと通る1点から求める方法
のとき公式が正しいことは簡単に確認できる。以下 とする。
の両辺を で微分すると,
よって,
なので,求める接線の傾きは, である。
よって,接線の方程式は,
が楕円上の点であることから,上式は,
となる。
円の結果を用いる方法
円の結果を用いる方法
中心が原点とは限らない楕円の接線
中心が原点とは限らない楕円の接線
中心が原点とは限らない,より一般的な楕円の接線の方程式です。
楕円 上の点 における接線の方程式は,
これも,冒頭の公式に(極線の方程式の証明と応用でも用いた)平行移動の議論を適用することで導けます。
まず図形全体を 方向に , 方向に 平行移動する。
楕円の式は ,点 は に移る。(これを点 とおく)
中心が原点である楕円の接線の方程式の公式を用いると,点 での接線の方程式 を得る。
図形全体を 方向に , 方向に 平行移動して元に戻すことで を得る。
なお,接する→重解→判別式が を用いて導出することもできます。











