関数の連続性と一様連続性
更新
-
が成立するとき,関数 が で連続という。 -
また,定義域(考えている区間内)の任意の点 で関数 が連続のとき, を連続関数と呼ぶ。
関数の連続性と一様連続性について「大雑把なイメージ」と「 を用いた厳密な定義」を説明します。
関数の連続性のイメージ
関数の連続性のイメージ
いきなり厳密な定義を書くと難しいので,まずはイメージから。
関数が連続であるとは,直感的には 「関数がつながっている,ちぎれていない」という意味です。
- は連続関数です。
- は原点で折れ曲がっているので微分不可能ですが,連続関数です。
- は連続関数です。
- も連続関数です。
なお,いたるところで不連続というヤバい関数もあります。→ディリクレ関数の定義と有名な3つの性質
ここまで理解できれば高校範囲では十分です。以下は大学内容です。
連続と一様連続の定義
連続と一様連続の定義
連続性をより厳密に定義します。そのためには,イプシロンデルタ論法を使います。 の参考には以下をどうぞ:
連続の厳密な定義
以下, は区間 上で定義された実数値関数とします。
関数 が で連続とは,任意の正の実数 に対して,ある正の実数 が存在して,任意の に対して なら が成立することを表す。
特に,すべての で が連続であるとき,関数 が区間 で連続という。
でつながっている。つまり「 が に十分近づくと も に近づく」ことを表しています。
一様連続
連続関数はつながっている関数なので扱いやすい嬉しい関数ですが,さらに 「一様連続関数」と呼ばれるもっと嬉しい関数のクラスがあります。連続であり,さらに 「十分」の程度が に依らないでおさえられるとき,一様連続と言います。
一様連続の方が強い条件です。
関数 が区間 で一様連続とは,任意の正の実数 に対して,ある正の実数 が存在して,
任意の実数 に対して, なら が成立することを表す。
非常に似ているので混乱しやすいです,じっくり考えてみてください。
- 「連続」の場合には場所 に応じて を持ってくる
- 「一様連続」の場合には場所によらない共通の を持ってくる
こうしてみると,一様連続のほうが強い定義であることがわかります。
つまり「一様連続関数は連続関数」ですが「連続関数が一様連続関数とは限らない」です。
関数の一様連続性のイメージ
関数の一様連続性のイメージ
連続だが一様連続でない例
連続と一様連続の違いは「連続だが一様連続でない例」を見ると理解できます。
例として を考えます。これは連続です。一方, が十分大きい時に猛烈に変化する(「十分」の程度がどこまでも厳しくなる)ので一様連続ではありません。
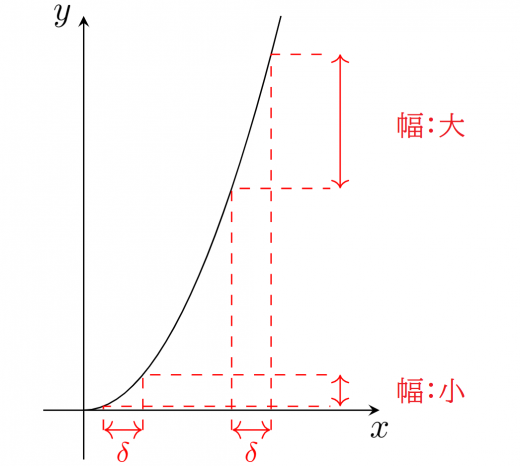
(場所によらない共通の を用意できないです)
これをきちんと証明してみましょう。
とする。
一様連続とは「 を任意にとるとき,ある があって であること」であった。
これの否定は「ある に対して,どのように をとっても とできない」こととなる。
とおいて考えてみると である。
今, と を1つ固定しておくと のとき, となる。
上記の考え方をもとに,きちんと証明を書くと以下のようになります。
とする。
を1つ決めたとき, をどのようにとっても,, ととれば, であるが, であるため, は一様連続ではない。
他の例
「一様連続」に関して他の例も見てみましょう。
- は一様連続関数です。
- は原点で折れ曲がっているので微分不可能ですが,一様連続関数です。
- は の近くで「十分」の程度がどこまでも厳しくなるので一様連続関数ではありません。
を用いた定義に従ってこれらの関数たちが連続,あるいは一様連続であることを証明してみてください。よい練習問題です。
有界閉区間上の連続関数
有界閉区間上の連続関数
は実数全体で考えると, が大きくなるにつれ,変化量が際限なく大きくなるため,一様連続ではなかったのでした。
一方 を に絞ると,変化量はたかが知れているので一様連続になります。
実は,より一般に以下の定理が成立します。
区間 上で定義された連続関数は 上で一様連続。
なぜ一様連続を考えるのか
なぜ一様連続を考えるのか
「連続関数では一般に成り立たず,一様連続関数だと成り立つ」ような嬉しい定理がいくつもあるので,一様連続という概念が重要になります。
より勉強したい人へ
より勉強したい人へ
連続関数の定義には区間が登場しました。この「区間」は「距離空間」というアイデアで拡張できます。
詳しくは 距離空間~位相空間論に向けた開集合・閉集合の一般化 を読んでみてください。
「連続」は局所的な概念,「一様連続」は大域的な概念です。











