チェバの定理:例題と3通りの証明
更新
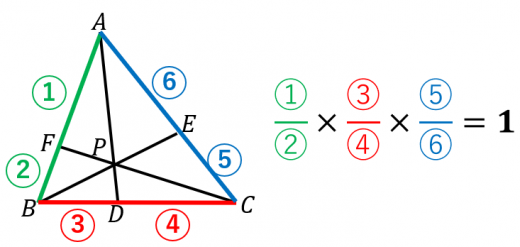
図において,
が成立する。これをチェバの定理と言う。
チェバの定理とは,三角形の周囲を1周しながら辺の比を取っていくと1になるという定理です。
チェバの定理の例題
チェバの定理の例題
チェバの定理は「線分の長さ」や「線分の比」を求めるために使われることが多いです。
のとき,
を求めよ。
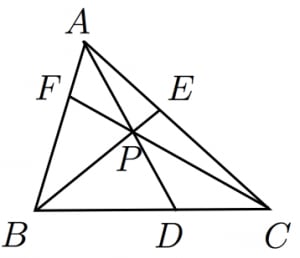
チェバの定理を使うと,
である。ここで,
- より
- より
すなわち,
したがって,,つまり
覚え方
覚え方
チェバの定理は 「三角形を1周しながら辺の比を取っていくと1になる」 と覚えましょう。

どこからはじめてもOKです! (図では頂点 からはじめて反時計回りに進んでいますが,別の点からはじめても,時計回りに進んでも同じ式になるので,細かい事は気にしなくて大丈夫です。)
チェバの定理の証明
チェバの定理の証明
チェバの定理の証明を3つ紹介します。
- 証明1:面積比による方法(有名)
- 証明2:メネラウスの定理を用いる方法
- 証明3:ベクトルによる方法(機械的に証明できる,計算が大変)
証明1. 面積比を用いる方法
有名なチェバの定理の証明です。
線分比を面積比に変換します。よく用いられる手法です。

三角形 の面積を などと書く。
黄色い三角形 と青い三角形 は,底辺 が共通で高さの比が なので,
つまり,
同様に,
以上3つの式を辺々かけ合わせると,
となり,チェバの定理を得る。
ちなみに,この証明方法の背景には,ベクトルの定番問題の公式(面積比)があります。三角形の中の点と3直線を見て連想できるとよいでしょう。
証明2. メネラウスの定理を用いる方法
メネラウスの定理を前提としたチェバの定理の証明です。

メネラウスの定理より,
上の式 下の式を計算すればチェバの定理となる。
証明3. ベクトルを用いる方法
計算がめんどうですが,機械的にチェバの定理を証明できます。
直線 と の交点を とおき, と の交点 が目標の比の式を満たしていることを証明します。これは同時にチェバの定理の逆の証明にもなっています。
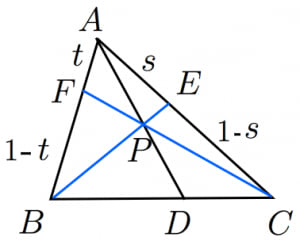
とおく。
となることを示せばチェバの定理が示される。
まずは と の交点 のベクトルを求める。
のベクトル方程式は,
のベクトル方程式は,
よって,
の係数を連立させて について解くと,
となるので,
よって,係数の比が となるのでチェバの定理が示された。
チェバの定理の逆
チェバの定理の逆
三角形の各辺上の点 に対して
ならば は一点で交わる。
高校入試・大学入試ではチェバの定理を使うことはあっても,その逆を使うことは少ないです。一方,数学オリンピックや難しい定理の証明では,むしろチェバの定理の逆が活躍します。3つの直線が1点で交わることの証明で活躍します。以下にチェバの定理の逆が使える4つの例を紹介します。
ベクトルは計算を省略しましたがそれでも長いです。初等幾何はひらめきが必要ですが美しいです。
Tag:とにかく美しい数学公式まとめ
Tag:有名な定理を複数の方法で証明
 メネラウスの定理とは,図において
メネラウスの定理とは,図において










