ケージーの定理とその証明
更新
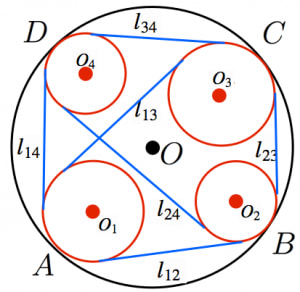
互いに交わらない4つの円 がそれぞれ点 で別の円 に(この順番に)内接しているとき,円 と の共通外接線の長さを とおくと,
図は複雑ですが,証明はかなりおもしろいです。数学オリンピックのよい練習問題ですので猛者は証明に挑戦してみてください。
定理の意味
定理の意味
-
互いに交わらない2つの円の共通外接線は2本ありますが,どちらを選んでも接点間の距離は同じなので が定義できます(共通内接線でないことに注意)。
-
4つの円の半径が無限小の場合を考えると,接線の長さは点の距離になります(例えば,)。 よって,この場合ケージーの定理はトレミーの定理と一致します。すなわち,ケージーの定理はトレミーの定理の一般化とみなせます。
ケージーの定理の証明の方針
ケージーの定理の証明の方針
ステップ1(普通):一気に証明するのは難しいので,まずは を評価しようと頑張ります。
そこで,余計な円 を排除した図を描くと,接する2つの円の相似の中心で紹介した頻出の構図であることが分かります。
よって, と の交点 は円 の円周上にあることが分かります。
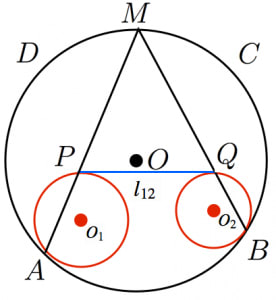
ステップ2(難): を評価しようと頑張ると,三角形 と が相似であることが分かります。
ステップ3(普通):次に,相似比を円の半径 を用いて表します。すると, という式が導けます。
ステップ4(易):残りの も同様に評価でき,トレミーの定理を用いるとケージーの定理が導かれます。
ケージーの定理の証明
ケージーの定理の証明

1:点 は円 と の相似の中心なので, と円 の交点 は, を満たす。同様に と円 の交点 も を満たす。よって である。
2:
より三角形 と は相似。
3:
同様に,
よって,相似比の二乗は,
これより
4: も同様に評価できる。
これと,トレミーの定理()より,ケージーの定理を得る。
4つの円の半径を小さくしていくとトレミーの定理になるというのは非常におもしろいです。











