二部グラフの最大マッチングと増加道
二部グラフにおける最大マッチング問題について,問題の意味とアルゴリズムをわかりやすく紹介します。
二部グラフ・マッチングとは
二部グラフ・マッチングとは
-
グラフとは,点の集合と枝の集合からなる「つながり方」を表すモデルです。
-
二部グラフとは,点が グループにわかれていて,同じグループ間はつながっていないようなグラフです。→グラフ理論の基礎
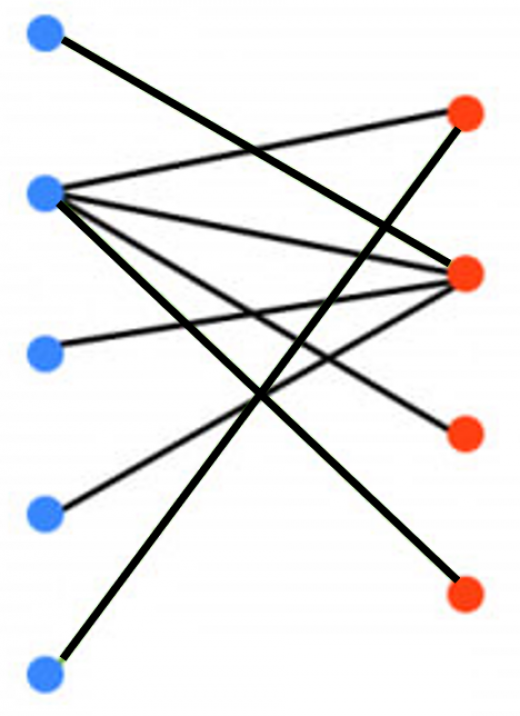
頂点が青と赤の2グループに分かれています。青同士、赤同士は枝で結ばれていないので二部グラフです。
- マッチングとは,端点を共有しない枝の集合です。
- グラフが与えられたときに要素数最大のマッチングを求める問題を最大マッチング問題と言います。マッチングは離散最適化の最も重要な話題の一つです。
例えば,左側の頂点を「男性」,右側の頂点を「女性」,「お互い付き合ってもよいペア」に枝を引いたグラフと見ると,カップル成立のペア数を最大化する問題です。

緑が最大マッチングの一例です。3ペアは可能ですが,4ペアはどうやってもできません。
増加道
増加道
最大マッチングを求めるアルゴリズムを説明するために必要な「増加道(増加路)」について説明します。
マッチング について以下を満たすとき 道 は増加道であるという。
- の出発点と到着点がマッチングの端点でない
- 交互路である( に含まれていない枝と含まれている枝を交互に使う)
例えば,下図左の「紫三角を端点とする長さ5の太線の道」は増加道です。
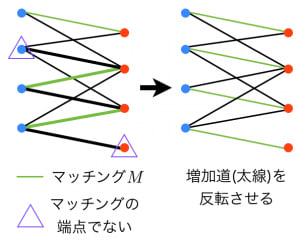
マッチング に対して増加道 を見つけることができれば の枝を「反転」させることで新たに要素数が1大きいマッチング を作ることができます。
つまり「増加道が存在→より大きなマッチングを作れる」というわけですが,実は逆も成り立つのです!
増加道に関する定理
増加道に関する定理
マッチング について,
増加道が存在しない は最大マッチング
増加道が存在すれば最大マッチングではないので,対偶を取ると が成立します。 の対偶「最大マッチングでないなら増加道が存在する」を証明します。
最大マッチングでないマッチング について増加道が存在することを証明する。真の最大マッチングを とする。
か のちょうど片方に属している枝の集合を (対称差と呼ばれる)とする。マッチングの性質より,一つの頂点に隣接している の枝は二本以下なので, はサイクルとパスに分解できる。
-
サイクルについて: の枝と の枝が交互に登場
-
パスについて: の枝からはじまり の枝で終わるパスが存在する( に注意)。
このパスこそが の増加道である。
最大マッチングを求めるアルゴリズム
最大マッチングを求めるアルゴリズム
次に,増加道の考え方を使った最大マッチングを求めるアルゴリズムを説明します。
-
適当に(最大でなくてもよい)マッチングを取ってくる
-
今持っているマッチングに対する増加道 を探して要素数が1大きいマッチングを得る。増加道を探す操作は,例えば幅優先探索でできる。
-
2を繰り返して増加道がなくなったら終了する
さきほどの定理のおかげで,最初にどんなマッチングを選んでも最終的に最大マッチングを見つけることができます。
注:二部グラフの最大マッチングは最大流問題の特殊ケースとみなせます。そのため,最大フローを求めるアルゴリズムを使うこともできます。おそらく最大フローを使う方が有名ですが,増加道の考え方がおもしろので紹介しました。
ちなみに,最大マッチング問題と似たような問題として,安定結婚問題があります。→安定マッチングとGale-Shapleyアルゴリズム
一般グラフになるとさらに楽しくなります!











