微分を用いた接線の方程式の公式
微分可能な関数
上の点
における接線の方程式は,
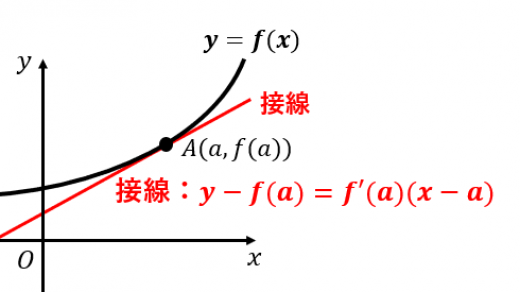
この公式の証明と,接線の方程式を求める問題2問を解説します。
接線の方程式の公式の導出
接線の方程式の公式の導出
証明と言うほどたいそうなものではありません,微分係数が接線の傾きであることで詳しく紹介しています。「微分係数=接線の傾き」を理解していればすぐに分かります。
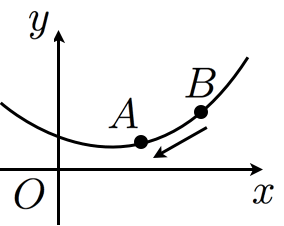
点 における微分係数 は(微分係数の定義より)図において を に近づけていったときの直線 の傾きの極限である。つまり, における接線の傾きは である。
傾きが で を通る直線の方程式は, である。これが求める接線の方程式。
このように一瞬で導出できるので,公式として丸暗記する必要はないです。考え方を理解しておきましょう。
二次関数の簡単な例題
二次関数の簡単な例題
二次関数 上の点 における接線の方程式を求めよ。
であり, における微分係数は である。
よって求める接線の方程式は,
つまり,
二次関数の接線は判別式を用いて求めることもできる。接線の方程式を とおくと,接線と二次関数の共有点は1つであるので,二次方程式 は重解を持つ。この二次方程式を整理すると,
この判別式が になるので,
よって,
つまり,求める接線の方程式は,
曲線外の点から引いた接線の方程式
曲線外の点から引いた接線の方程式
三次関数 のグラフに から引いた接線の方程式を求めよ。
三次関数 の導関数は である。よって, における接線の方程式は,
これが を通るとき
これを整理すると,
実数解は のみ。
よって,接点の座標は となり,接線の方程式は となる。
注:三次方程式の解き方は三次方程式の解き方3パターンと例題5問をどうぞ。関連する話題として三次関数の接線の本数についての美しい定理もどうぞ。
高校数学では登場しない大道具を使ってみましょう。
二次関数の場合と同じく三次関数の場合も判別式で強引に解ける。
接線の方程式を とおくと,三次方程式
は重解を持つ。この方程式を整理すると,
この判別式(→三次方程式の判別式)が になるので,
この三次方程式を頑張って解くと,実数解は のみであることが分かる。よって,接線の方程式は
→高校数学の問題集 ~最短で得点力を上げるために~のT76では,さらなる別解と計算ミスをしないためのコツも紹介しています。
円の接線の方程式について
円の接線の方程式について
接線の方程式といえば,今回紹介した だけではなく,円の接線の方程式の公式も重要です。
座標平面において,円: 上の点 における接線の方程式は,
美しい公式です。この公式については,円の接線の方程式を求める公式の3通りの証明で詳しく紹介しています。
三次方程式の判別式が登場しましたが,二次の係数が でない三次方程式の判別式は複雑なので使わない方がよいです。











