ベルンシュタインの定理とその証明

開区間から閉区間への単射は，$f(x)=x$ とすればよい。

閉区間から開区間への単射は，例えば $g(x)=\dfrac{x}{2}+0.1$ とすればよい。

よって，ベルンシュタインの定理により全単射の存在が示された。

記述の都合上，$A$ と $B$ が共通の要素をもたない場合について証明する（このようにしても一般性を失わない）。

$A$ から $B$ への単射を $f$ ，$B$ から $A$ への単射を $g$ とする。

$A\cup B$ を「 $f$ または $g$ を何回かかましてうつるものは仲間」という基準でグループ分けする（図参照）。

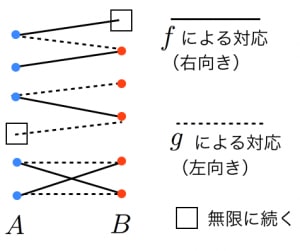
$f,g$ はともに単射なので，図において，各頂点から辺は高々2本しか出ていない。よって，1つのグループには1つのパス（長さは無限）またはサイクルが対応する。以下では，$A$ から $B$ への全単射を，各グループごとに構成する。

• パスの片方の端点が $A$ に属するグループ（図の一番上のようなグループ）$f$ を使えばよい。

• パスの片方の端点が $B$ に属するグループ（図の上から２番目のようなグループ）$g^{-1}$ を使えばよい。

• パスが両側に無限に続くグループ $f$ または $g^{-1}$ を使えばよい。

• サイクルに対応するグループ（図の一番下のようなグループ）$f$ または $g^{-1}$ を使えばよい。