内接円に関する数オリ頻出の図形

三角形 の内接円と辺 の接点を とおく。 から辺 と垂直な直線と内接円の交点を とおく。さらに と の交点を とおくと,
この定理の2通りの証明を紹介します。
応用例として,国際数学オリンピックの過去問も解説します。
定理の証明その1
定理の証明その1
まずは愚直に計算する方法です。少し大変ですが,ほとんど機械的な計算で証明できます。
三角形 の情報で全ての長さを表していきます。 は 傍心の意味と性質・内心との比較の公式から瞬時に求まります。あとは の長さを求めればよいのですが,直角三角形の1辺である の方が計算しやすそうなので頑張って を計算します。
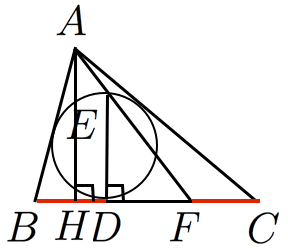
三角形の3辺の長さを とおく。
のときは二等辺三角形となり自明なので,対称性より の場合のみ証明すればよい。
内接円の性質より
とおき, を求めにいく。
から に引いた垂線の足を とおくと,三角形 と は相似なので
これに,
を代入すると,
余弦定理を用いて を消去する:
右辺が因数分解できて が分かる。
よって
定理の証明その2
定理の証明その2
相似を用いたおもしろい方法です!
内接円と傍接円の共通外接線の交点が なので は2つの円の相似の中心です。(直感的に明らかですが,気になる人は2つの円の相似の中心を参考に座標を用いて証明してみてください。)
数オリの問題に挑戦
数オリの問題に挑戦
1992年国際数学オリンピックロシア大会の第4問です。
円 の接線 上に点 がある。以下の条件を満たす点 の存在範囲を求めよ。
「 上に 点 が存在して, かつ が三角形 の内接円」
上記の定理を知っていればさきほどの図形が浮かんできます!
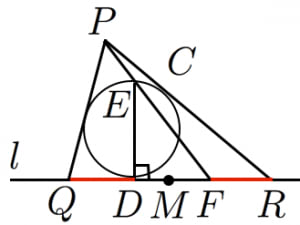
はさきほどと同様。 は に関して と対称な点とする。
答えは「 が直線 上で に関して と反対側にあるとき(A)」である。
・条件を満たすなら(A)が成立すること
と の交点を とおく。さきほどの定理より
条件を満たすとき, なので であり,
つまり と の交点は に関して と対称な点。
・(A)が成立するなら条件を満たすこと
さきほどの定理より よって となり は条件を満たす。
マニアックな形に見えますが結構よく出る構図です。
Tag:国際数学オリンピックの過去問










