美術館定理とその証明

更新 2021/03/07

美術館定理

穴のない $n$ 角形の全領域を監視するために必要な監視カメラの台数は高々 $\left\lfloor\dfrac{n}{3}\right\rfloor$ 台

美術館問題（Art Gallery Problem）

平面上に穴のない nnn 角形がある（へこんでいてもよい，美術館の図面と思って下さい）
この全領域を見渡せるように監視カメラを設置したい
監視カメラは 360360360 度見渡せるものとする
監視カメラの台数はできるだけ少なくしたい，何台必要か？　どのように配置すればよいか？
例えば図のような八角形の場合，赤い点のところに設置すればOKなので，三台あれば十分です。実はうまくやれば二台で十分です。
以下では必要な台数と設置方法について考えます。

美術館定理

定理1

美術館が穴のない $n$ 角形なら $\left\lfloor\dfrac{n}{3}\right\rfloor$ 台あれば十分。

ただし， $\lfloor x\rfloor$ は $x$ の整数部分を表す記号です。→ガウス記号の定義と3つの性質

証明の概要

美術館を適当に三角形分割する。この三角形分割された図において，各辺の両端が異なる色であるように頂点を三色に塗り分けることができる（→注）

美術館の三角形分割

三色の中で一番少ないものは $\left\lfloor\dfrac{n}{3}\right\rfloor$ 個以下である。その色を赤とする。赤い頂点のところに監視カメラをおけばOK。

なぜなら，全ての三角形についていずれかの頂点は赤色であるので，どの三角形内もいずれかの赤色の点から監視できる。

最後に注の部分「穴のない $n$ 角形を三角形分割したグラフが3彩色可能である」を証明して定理1の証明を完成させます。なお，点と線からなる離散構造をグラフと言います。→グラフ理論の基礎

注の証明

帰納法で証明する。三角形 $1$ 個からなるグラフは明らかに3彩色可能。

三角形 $n$ 個からなるグラフが3彩色可能だと仮定する。 $n+1$ 個の三角形に分割されたグラフについて，一つの三角形としか隣接していない三角形が存在する（もしそうでないと，三角形たちで「ループ」ができるので内側に頂点が追加されてしまう or 穴ができてしまう）

この三角形を除いたグラフは帰納法の仮定により3彩色可能である。最後に $n+1$ 個目の三角形をつけ加えた際に，新たに追加された頂点を適切な色で塗れば全体としても3彩色可能である。

以上の証明から分かるように，適当に三角形一つからスタートして次々に三角形を貼りあわせていきながら彩色してくことで，全体を3彩色することができます。3彩色が分かれば $\left\lfloor\dfrac{n}{3}\right\rfloor$ 台以下で全領域を監視できるようなカメラの設置場所も分かります！

最悪ケース

定理2

任意の $3$ の倍数 $n$ に対して監視カメラが $\dfrac{n}{3}$ 台必要になるような残念な形が存在する。

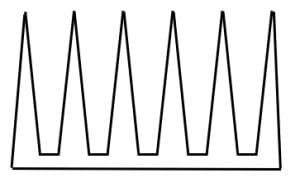
残念な美術館

図のような「くし型」の場合，一台で2つ以上のトゲを監視することはできないので，カメラがトゲの数だけ必要です。図は $n=6$ の場合です。18角形で6台必要です。

ただし，実際はくし形の美術館なんて存在しませんね。

知人のU氏と読者の方に独立同時期に提供していただいたネタです，感謝！

Tag:数学の定理No.1決定戦

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！