逆三角関数(Arcsin,Arccos,Arctan)の意味と性質

更新 2023/08/10

逆三角関数

逆三角関数(Arcsin,Arccos,Arctan)とは，三角関数 $\sin x,\cos x,\tan x$ の逆関数のことです。

逆三角関数の意味と性質をわかりやすく解説します。

Arcsin とは sin の逆関数

Arcsin とは

$\sin x\:\left(-\dfrac{\pi}{2}\leq x\leq\dfrac{\pi}{2}\right)$ の逆関数を $\mathrm{Arcsin}\:x$ または $\sin^{-1}x$ と書くことがあります。

逆関数なので「 $x$ と $y$ が交換」されます。例えば， $\sin\dfrac{\pi}{4}=\dfrac{\sqrt{2}}{2}$ なので， $\mathrm{Arcsin}\dfrac{\sqrt{2}}{2}=\dfrac{\pi}{4}$ です。
$\mathrm{Arcsin}\:x$ とは， $\sin y=x$ を満たす $y$ のこと（ただし， $-\dfrac{\pi}{2}\leq y\leq\dfrac{\pi}{2}$ の範囲）とも言えます。
$y=\sin x$ の逆関数は，そのままでは考えられません（ $y$ を決めたときに $y=\sin x$ を満たす $x$ が1つに決まらない）。そこで，定義域を $-\dfrac{\pi}{2}\leq x\leq\dfrac{\pi}{2}$ に限定することで逆関数を考えています。→逆関数の3つの定義と使い分け

例題

$\mathrm{Arcsin}\:\dfrac{1}{2}$ を求めよ。

解答

$\sin x=\dfrac{1}{2}$ を満たす $x$ で $-\dfrac{\pi}{2}\leq x\leq\dfrac{\pi}{2}$ の範囲内のものは， $x=\dfrac{\pi}{6}$ なので， $\mathrm{Arcsin}\:\dfrac{1}{2}=\dfrac{\pi}{6}$

$y=\mathrm{Arcsin}\:x$ のグラフは図のようになります。定義域は $-1\leq x\leq 1$ で，値域は $-\dfrac{\pi}{2}\leq y\leq\dfrac{\pi}{2}$ です。

Arccos とは cos の逆関数

Arccos とは

$\cos x\:\left(0\leq x\leq\pi\right)$ の逆関数を $\mathrm{Arccos}\:x$ または $\cos^{-1}x$ と書くことがあります。

例えば， $\cos\dfrac{\pi}{4}=\dfrac{\sqrt{2}}{2}$ なので， $\mathrm{Arccos}\dfrac{\sqrt{2}}{2}=\dfrac{\pi}{4}$ です。
$\mathrm{Arccos}\:x$ とは， $\cos y=x$ を満たす $y$ のこと（ただし， $0\leq y\leq\pi$ の範囲）とも言えます。
$\sin$ の場合と同じく， $y=\cos x$ の逆関数は，そのままでは考えられません。そこで，定義域を $0\leq x\leq\pi$ に限定して逆関数を考えます。
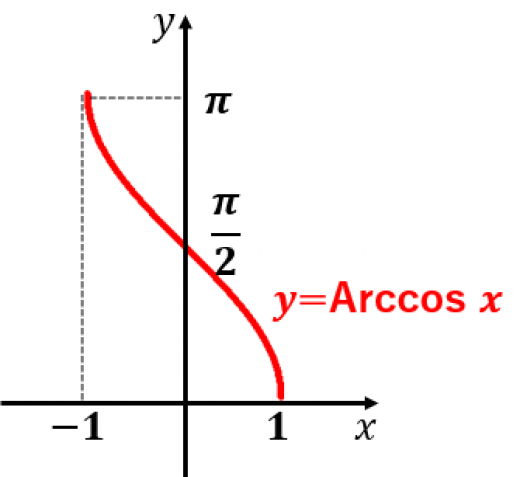
$y=\mathrm{Arccos}\:x$ のグラフは図のようになります。定義域は $-1\leq x\leq 1$ で，値域は $0\leq y\leq\pi$ です。

Arctan とは tan の逆関数

Arctan とは

$\tan x\:\left(-\dfrac{\pi}{2} < x <\dfrac{\pi}{2}\right)$ の逆関数を $\mathrm{Arctan}\:x$ または $\tan^{-1}x$ と書くことがあります。

$\mathrm{Arctan}\:x$ とは， $\tan y=x$ を満たす $y$ のこと（ただし， $-\dfrac{\pi}{2}< y < \dfrac{\pi}{2}$ の範囲）とも言えます。
$y=\mathrm{Arctan}\:x$ のグラフは図のようになります。定義域は実数全体で，値域は $-\dfrac{\pi}{2} < x <\dfrac{\pi}{2}$ です。

以上 $3$ つ（ $\mathrm{Arcsin},\mathrm{Arccos},\mathrm{Arctan}$ ）を合わせて逆三角関数と呼びます。

逆三角関数のグラフ

すでに登場しましたが，逆三角関数のグラフを3つ書いてみます。逆関数のグラフはもとの関数のグラフを
y=xy=xy=x
 に関して折り返したものなので，逆三角関数のグラフは図のようになります。
赤が
y=Arcsin xy=\mathrm{Arcsin}\:xy=Arcsinx
青が
y=Arccos xy=\mathrm{Arccos}\:xy=Arccosx
緑が
y=Arctan xy=\mathrm{Arctan}\:xy=Arctanx
です。

逆三角関数の微分

$y=\mathrm{Arcsin}\:x$ のとき $y'=\dfrac{1}{\sqrt{1-x^2}}$

$y=\mathrm{Arccos}\:x$ のとき $y'=-\dfrac{1}{\sqrt{1-x^2}}$

$y=\mathrm{Arctan}\:x$ のとき $y'=\dfrac{1}{1+x^2}$

逆関数の微分を求めるよい練習問題です。入試でも逆三角関数の微分にまつわる問題がたまに出題されます。→逆関数の微分公式を例題と図で理解する

Arcsinの微分の証明

$y=\mathrm{Arcsin} x$

のとき $x=\sin y$ の両辺を $x$ で微分して，

$1=y'\cos y$

よって $y'=\dfrac{1}{\cos y}$

また， $-\dfrac{\pi}{2}\leq y\leq \dfrac{\pi}{2}$ より，

$\cos y=\sqrt{1-\sin^2 y}=\sqrt{1-x^2}$

$\mathrm{Arccos}$ についても同様です。

Arctanの微分の証明

$y=\mathrm{Arctan} x$

のとき $x=\tan y$ の両辺を $x$ で微分して，

$1=y'\dfrac{1}{\cos^2 y}$

よって $y'=\cos^2 y=\dfrac{1}{1+\tan^2y}=\dfrac{1}{1+x^2}$

逆三角関数にまつわる積分公式

逆三角関数の積分

$\displaystyle\int\mathrm{Arcsin}\:xdx=x\mathrm{Arcsin}\:x+\sqrt{1-x^2}+C$

$\displaystyle\int\mathrm{Arccos}\:xdx=x\mathrm{Arccos}\:x-\sqrt{1-x^2}+C$

$\displaystyle\int\mathrm{Arctan}\:xdx=x\mathrm{Arctan}\:x-\dfrac{1}{2}\log(1+x^2)+C$

さきほどの逆三角関数の微分公式と合成関数の微分を用いて右辺を微分すると，左辺と一致することが分かります。

以下のように部分積分を使って導出することもできます。

Arcsin の積分の導出

$\displaystyle\int 1\cdot \mathrm{Arcsin}\:xdx\\ =x\mathrm{Arcsin}\:x-\displaystyle\int x\cdot\dfrac{1}{\sqrt{1-x^2}}dx\\ =x\mathrm{Arcsin}\:x+\dfrac{1}{2}\displaystyle\int(1-x^2)'\cdot\dfrac{1}{\sqrt{1-x^2}}dx\\ =x\mathrm{Arcsin}\:x+\sqrt{1-x^2}+C$

Arccos の積分の導出

$\displaystyle\int 1\cdot \mathrm{Arccos}\:xdx\\ =x\mathrm{Arccos}\:x+\displaystyle\int x\cdot\dfrac{1}{\sqrt{1-x^2}}dx\\ =x\mathrm{Arccos}\:x-\dfrac{1}{2}\displaystyle\int(1-x^2)'\cdot\dfrac{1}{\sqrt{1-x^2}}dx\\ =x\mathrm{Arccos}\:x-\sqrt{1-x^2}+C$

Arctan の積分の導出

$\displaystyle\int 1\cdot \mathrm{Arctan}\:xdx\\ =x\mathrm{Arctan}\:x-\displaystyle\int x\cdot\dfrac{1}{1+x^2}dx\\ =x\mathrm{Arccos}\:x-\dfrac{1}{2}\displaystyle\int(1+x^2)'\cdot\dfrac{1}{1+x^2}dx\\ =x\mathrm{Arccos}\:x-\dfrac{1}{2}\log(1+x^2)+C$

逆三角関数に関係する積分

$\displaystyle\int\dfrac{1}{\sqrt{a^2-x^2}}dx=\mathrm{Arcsin} \dfrac{x}{a}+C$

$\displaystyle\int\dfrac{1}{a^2+x^2}dx=\dfrac{1}{a}\mathrm{Arctan} \dfrac{x}{a}+C$

こちらも，さきほどの逆三角関数の微分公式と合成関数の微分を用いて右辺を微分すると，左辺と一致することが分かります。

このように不定積分にすると $\mathrm{Arcsin}$ などが明示的に出てしまうので高校数学の範囲では定積分しか出題されません。

$\dfrac{1}{\sqrt{a^2-x^2}}$ の定積分は $x=a\sin\theta\:(x=a\cos\theta)$ と置換するとうまくいく。
$\dfrac{1}{a^2+x^2}$ の定積分は $x=a\tan\theta$ と置換するとうまくいく。

というのは逆三角関数の微分公式のおかげということですね。

三角関数の「逆関数」を紹介しました。三角関数の「逆数」は，また別の関数になります。→sec, cosec, cotと記号の意味

Tag:数検1級の範囲と必要な公式まとめ

Tag:積分公式一覧

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！