アポロニウスの円の証明と応用
アポロニウスの円について紹介します。
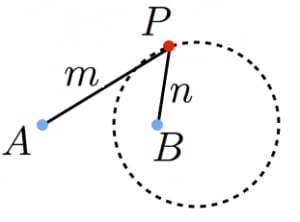
2点 からの距離の比が で一定である点の軌跡は円である。これをアポロニウスの円と呼ぶ。
なお, のときの軌跡は の垂直二等分線になりますが,これを半径無限大の円とみなすとアポロニウスの定理は崩れません。
アポロニウスの円の座標による証明
アポロニウスの円の座標による証明
座標を設定すれば機械的な計算でアポロニウスの円が導出できます。
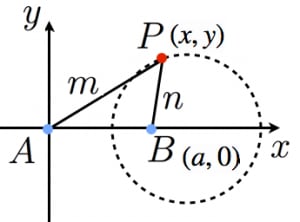
のときは自明なので, としても一般性を失わない。
として
であることの必要十分条件は
これは, の係数と の係数が等しく の項が現れない二次曲線なので明らかに円である。(→注)
そして, の一次の項も現れないので円の中心は 軸上にある。
これでアポロニウスの円の証明になっていますが,円の中心と半径を明示的に求めたい場合は平方完成する必要があります。
注:厳密には「 の係数と の係数が等しく の項が現れない」だけでは不十分です(例えば, を満たす点は存在しない)。これに対する説明としては,実際に平方完成する or 「 を に内分する点および外分する点は軌跡上にあり,軌跡は2点以上を含むので右辺の定数部分が負になることはない」といえばOKです。
アポロニウスの円の応用
アポロニウスの円の応用
私は高校生のときはアポロニウスの円の何が嬉しいか分かりませんでした。しかし,アポロニウスの円の知識を使うことで以下の有用な定理が証明できるのです!
4点 がこの順に同一直線上にあり, を満たしている。また,線分 を直径とする円 上に点 を取る。
すると,
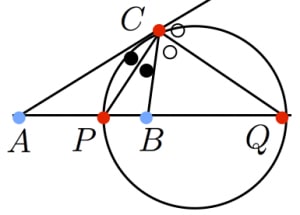
点 からの距離の比が であるような点の軌跡はアポロニウスの定理より円である。そして はその円周上にある。また,アポロニウスの円の直径は直線 上にあるので が直径である。
つまり,円 はアポロニウスの円そのものである。
よって円上の任意の点 に対して が成立する。
これと角の二等分線定理の逆より定理が証明された。
→高校数学の問題集 ~最短で得点力を上げるために~のT140では,アポロニウスの円に関する問題と計算ミスを減らすコツを紹介しています。
次に,上記の定理の嬉しさについて解説します。
アポロニウスの円と調和点列
アポロニウスの円と調和点列
上記の定理の仮定を満たすような図形は数学オリンピックなどの問題ではしばしば出現します!
「4点 がこの順に同一直線上にあり, が成立する」とき を調和点列と呼びます。
調和点列はいろいろなところに出現する上にいろいろな定理が使える重要な構図です。
その定理の一つがアポロニウスの円を利用した上記の定理なのです。
標語的に言えば 「調和点列と円があれば等しい角が隠れている」ということになります。
今後は調和点列についても紹介していきたいと思っています!











