8パズル，15パズルの不可能な配置と判定法

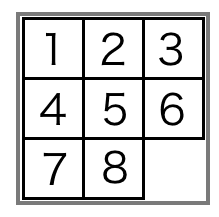
• 8パズル，15パズルはパネルをスライドさせて目標の形（図の形）を作るゲームです。名前は知らないかもしれませんが，ほとんどの人が一度はやったことがあるゲームだと思います。
• 8パズル，15パズルの解析には置換とそのパリティ（奇置換，偶置換）の知識を使います。知らなくても雰囲気は分かりますが，きちんと理解するためには置換の知識が必須です。→置換の基礎（互換・偶置換・奇置換・符号の意味）

8パズルも15パズルも同じように扱えるので，8パズルで解説します。

まず，8パズルの状態に対応する9次元ベクトル（9個の数字の並び）を考えます。左上から右下に向かって，どの数字が入っているのか順番に書き並べます（パネルがない「空き」の場所には9を入れます）。

例えば，図1の状態に対応するベクトルは，$(1,2,3,4,5,6,8,7,9)$ です。図2の状態に対応するベクトルは，$(2,1,3,4,9,6,7,8,5)$ です。

初期状態に対応するベクトルを $s$，完成した状態に対応するベクトルを $t=(1,2,3,4,5,6,7,8,9)$ と書くことにします。

例えば，上記の図1は「完成不可能な配置」です。実際，

• $s$ を $t$ にするには $7$ と $8$ を交換するだけでよい。互換一回で表せるので定理の左辺（置換のパリティ）は奇。
• 「空き」の位置はスタートとゴールで同じ位置なので最短距離は $0$，すなわち偶。

一方，上記の図2は「完成可能な配置」です。実際，

• $s$ を $t$ にするには $(1,2),(5,9)$ を交換すればよい。互換二回で表せるので置換のパリティは偶。
• 「空き」の位置はスタートとゴールで横に1，縦に1ズレている。最短距離は $2$，すなわち偶。

また，15パズルでも同じ定理が成立します。より一般に $M\times N$ パズル $(M,\:N\geq 2)$ でも同じ定理が成立します。この定理を認めれば，冒頭の主張は直ちに導かれます。冒頭の主張では置換のパリティは奇で空きの最短距離は0だからです。

実際に与えられた配置が可能かどうかは，上記の定理を使って簡単に判定できます。

• 空きの最短距離はすぐに分かります。数えて下さい。

• 初期状態 $s$ と完成状態 $t$ の置換のパリティを求めるためには，実際に $s$ を $t$ にする置換を互換たちで表してその偶奇を見ればOKです。これは置換をサイクル分解してもできますし，以下のように1から順番にそろえていってもOKです。

定理の $\Rightarrow$ を証明します。

なお，$\Leftarrow$ については構成的に（偶奇が一致するときに8パズルを完成させるアルゴリズムを与える）証明できたつもりになっていますが，きちんと書くと煩雑なので省略します。

Tag:難しめの数学・雑学ネタまとめ